Metrics

Below we provide a number of metrics that have been defined on curricula and degree plans. These metrics are used to compute the overall complexity of curricula and degree plans after you upload them.

Note: In order to better understand the various metrics described below, you may wish to first review the basic terminology associated with curricular analytics.

Curricular Metrics

Curriculum-based metrics are based upon the graph structure of a curriculum. Specifically, assume curriculum $c$ consists of $n$ courses $\{c_1, \ldots, c_n\}$ , and that there are $m$ requisite (prerequisite or co-requsitie) relationships between these courses. A curriculum graph $G_c = (V,E)$ is formed by creating a vertex set $V = \{v_1, \ldots, v_n\}$ , i.e., one vertex for each course, along with an edge set $E = \{e_1, \ldots, e_m\}$ , where a directed edge from vertex $v_i$ to $v_j$ is in $E$ if course $c_i$ is a requisite for course $c_j$ .

Blocking Factor

The blocking factor is an important curriculum-based metric because it measures the extent to which one course blocks the ability to take other courses in the curriculum. That is, a course with a high blocking factor acts as a gateway to many other courses in the curriculum. Students who are unable to pass the gateway course will be blocked from taking many other courses in the curriculum.

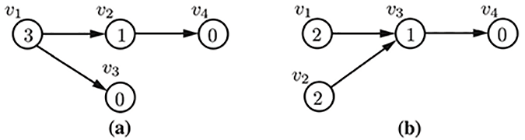
We define the blocking factor of a course $c_i$ as the number of courses in the corresponding curriculum graph that are reachable from $v_i$ . As examples of the blocking factor metric, conisder the two four-course curricula graphs, with course vertices $v_1, v_2, v_3$ and $v_4$ , shown below. In part (a) of this figure, $v_1$ is a prerequisite for courses $v_2$ and $v_3$ , and $v_2$ is a prerequisite for course $v_4$ , while in part (b), courses $v_1$ and $v_2$ are prerequisites for course $v_3$ , and $v_3$ is a prerequisite for course $v_4$ . The blocking factor of each course are shown inside of the course vertices in this figure.

Delay Factor

Many curricula, particularly those in science, technology engineering and math (STEM) fields, contain a set of courses that must be completed in sequential order. The ability to successfully navigate these long pathways without delay is critical for student success and on-time graduation. If any course on the pathway is not completed on time, the student will then be delayed in completing the entire pathway by one term. The delay factor metric allows us to quanity this effect.

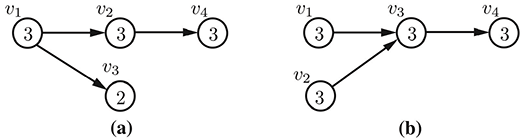
We define the delay factor of course vertex $c_i$ to be the length of the longest path in the corresponding curriculum graph that contains $v_i$ . As an example of the delay factor metric, consider the same four-course curricula shown above. The delay factor of each course are shown inside of the course vertices in the figure below.

Centrality

A course can be thought of as being central to a curriculum if it requires a number of foundational courses as prerequisites, and the course itself serves as a prerequisite to many additional discipline-specific courses in the curriculum. The centrality metric is meant to capture this notion.

We define the centrality of source and sink vertices to be 0. For all other course vertices, consider all of the long paths (i.e., unique paths from a source to a sink) containing course vertex $v_i$ . The centrality of $v_i$ is given by the sum of these path lengths. As an example of the centrality metric, consider the same four-course curricula shown above. The centrality factor of each course are shown inside of the vertices in the figure below. In the case of the curriculum in part (a), there is one long path of length three that includes course $v_2$ , hence its centrality is 3, while in part (b), there are two long paths of length three that include course $v_2$ , hence its centrality is 6.

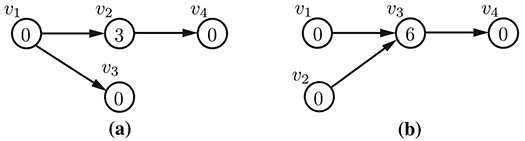
Structural Complexity

The curricular complexity of a course is meant to capture the impact of curricular structure on student progression. Through experimentation, we have found that a simple linear combination of the delay and blocking factors described above provides a good measure for quantifying the structural complexity of a curriculum. Specifically, we have found a high correlation between increased structural complexity and decreased graduation rates.

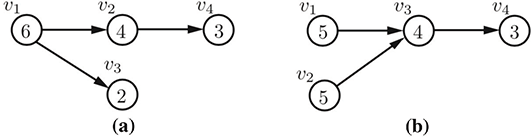
As an example of the structural complexity metric, consider the same four-course curricula shown above. The compleixty factor of each course, which is simply the sum of the course's delay and blocking factors, are shown inside of the course vertices in this figure.

Degree Plan Metrics

The aforementioned curricular complexity metrics are independent of how a curriculum is layed out as a degree plan. That is, the curricular metrics will not change as different degree plans are created. Degree plan metrics are related to the manner in which courses in the curriculum are laid out across the terms in the degree plan. These metrics are used in the creation of optimal degree plans as described in Optimized Degree Plans.